كاربرد نظريه ي سوال پاسخ در كشف ژن هاي غالب و برآورد استعداد افراد در فعال سازي ژن ها

نویسنده و مسول مقاله: محمد حسین ضرغامی (دکتری سنجش و اندازه گیری)

چکیده: اين پژوهش روشي را براي تحليل ويژگي هاي دسته اي از ژن ها كه اثر مشخصي روي يك بيماري يا اختلال دارند، معرفي مي كند. در اين روش از نظريه ي سوال پاسخ در برآورد پارامترهاي ژن و همچنين پارامتر استعداد يا زمينه ي فرد استفاده مي شود. نحوه ي عملي برآورد پارامترهاي ژن و فرد از طريق داده هاي شبيه سازي شده نشان داده شده است. خروجي نهايي نرم افزار مقادير عددي پارامترها مي باشد كه مي تواند در تهيه ي بانك ژن و پيش بيني فعال سازي ژن ها توسط افراد با زمينه هاي مختلف مورد استفاده قرار گيرد.

مقدمه

در بیشتر موقعیت های عملی تصمیمات بر اساس کمیت هایی گرفته مي شود که نمی توان آنها را به طور مستقیم مشاهده نمود. این کمیت ها به متغیرهای مکنون  مشهورند. هر مدلی که یک ساختار پنهان را به یک ساختار مشاهده شده مربوط کند، مدل متغییر مکنون  نام دارد(برسبوم ، 2005). چون متغییرهای مکنون در حوزه های علمی مختلف مورد مطالعه می باشند، مدل های متغییر مکنون در حوزه های مختلف علوم کاربرد دارند. متغیرهای پنهان یا مکنون در روانشناسی توانایی، صفات و نگرش، در بازاریابی قدرت خرید، در زیست شناسی کیفیت زندگی یا زمینه ی یک بیماری خاص می باشند.

در آمار متغير مكنون متغيري است كه مستقيما مشاهده نمي شود اما بوسيله ي اعمال مدل هاي آماري و رياضي  روي داده هاي مشاهده شده قابل استنباط مي باشند. البته شرايط ويژه اي براي مكنون بودن يك متغير وجود دارد كه در اين مقاله قصد پرداختن به آن نيست(رجوع به برسبوم، 2008). مدل هاي رياضي آماري كه هدف آنها توضيح متغيرهاي مشاهده شده از طريق متغيرهاي مكنون است به مدل هاي متغير مكنون رياضي آماري معروف اند(برسبوم، 2008). 

مدل هاي مكنون بر اساس نوع متغير پنهان و داده هاي مشاهده شده كه ورودي هاي مدل محسوب مي شوند، انواع مختلفي دارند. در جدول زير اين طبقه بندي مشخص شده است.

جدول 1: طبقه بندي مدل هاي متغير مكنون

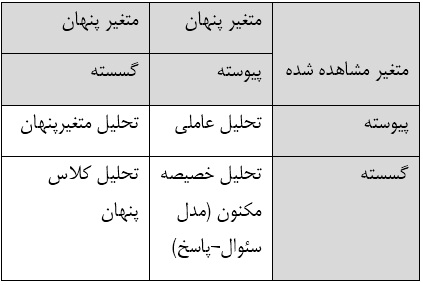
مدل سوال پاسخ 

یکی از مدل های متغیر مکنون مدل هاي سوال پاسخ مي باشند که مبتنی بر نظریه ی سوال پاسخ اند. این نظریه دو مفروضه ی اساسی دارد. الف) عملکرد آزمودنی در هر آیتم  می تواند به وسیله ی مجموعه ای از عوامل که صفات یا صفات مکنون نامیده می شود، پیش بینی و توضیح داده شود و ب) رابطه میان عملکرد آزمودنی در یک آیتم به وسیله یک تابع تکنوا افزایشی که تابع ویژه آیتم یا خم ویژه آیتم نامیده می شود، قابل توصیف است(همبلتون و سواميناتان ، 1985). این تابع مشخص می کند که هر چه سطح صفت در آزمودنی بالاتر رود پاسخ مثبت به محرك نیز افزایش پیدا می کند.  مدل هاي سوال پاسخ بر مبنای مجموعه ای از متغیرها، به نام آیتم بنا می شوند. 

بنابراین مسئله در مدل های سوال پاسخ به دو موضوع اصلی مربوط می شود، یکی آزمودنی (مانند انسان، حیوان و یا گیاه) و دیگر آیتم (مانند سوال، ژن و یا یک تکلیف مشخص). درحوزه ی اندازه گیری آموزشی  سوالات یک آزمون و افرادي كه به سوالات پاسخ مي دهند به ترتيب آيتم ها و آزمودني هاي مطالعه را تشكيل مي دهند. در زيست شناسي مولكولي و ژنتيك ، ژن های موثر در یک بیماری و نمونه هاي زيستي، آيتم ها و آزمودني هاي مدل اند.  

آزمودنی ها و آیتم های موجود در یک مطالعه پارامترهای خاص خود را دارند. بر اساس این پارامترها برای هر آیتم می توان تابع ویژه آن را ترسیم نمود به طوری که بر اساس آن احتمال ظهور و بروز صفت در آزمودنی های مختلف مشخص می شود. در اندازه گیری آموزشی تابع ویژه ی آیتم همان تابع ویژه ی سوال است که بر اساس آن احتمال پاسخ صحیح به یک سوال برای آزمودنی های مختلف با سطح توانایی متفاوت تعیین می شود. در مطالعات بازاریابی تابع ویژه ی آیتم سطح دانش فرد در مورد یک محصول خاص، احتمال خرید آن محصول خاص را مشخص می کند. در زيست شناسي ملكولي و ژنتيك بر اساس تابع ویژه ی ژن می توان احتمال روشن شدن ژن را برای افراد با زمینه و استعداد متفاوت نشان دهد(تاوارس  و همكاران، 2004). 

مزیت استفاده از مدل هاي سوال پاسخ تنها به مشخص ساختن رابطه ي احتمالي بين آيتم ها و آزمودني ها محدود نمی شود. برآورد پارامتر آیتم ها و آزمودنی ها تحت این مدل نیز می تواند به مطالعه ی آنها کمک نماید. به عنوان مثال می توان از طریق  مجموعه ای از ژن ها، زمینه  یا استعداد  یک فرد در یک بیماری خاص را كه نشان دهنده ي پتانسيل ابتلاء به آن بيماري است، مشخص نمود. علاوه بر اين در مطالعات سيستماتيك جانوري يا گياهي مي توان احتمال بروز يك صفت خاص، يا درجاتي از آن را بررسي كرد. در این مثال آیتم ها همان ژن ها هستند و پاسخ آنها می تواند فعال  یا غیر فعال  و یا نشان دهنده ی درجه ای از فعالیت باشد که از نظر شدت در طبقات مختلف قرار می گیرند و بنابراين امكان استفاده از نظريه ي سوال پاسخ براي داده هاي بيان ژن  مهيا مي شود. در اين صورت سطح بيان  به عنوان پاسخ يك نمونه بيولوژيكي خاص به يك ژن خاص تعريف مي شود. ژن ها دارای پارامترها (ویژگی ها)ی خاص خود می باشند که باید در مدل وارد شوند. در پژوهش حاضر روش سوال پاسخ برای تحلیل ویژگی های یک مجموعه از ژن ها که می توانند در یک بیماری خاص تاثیر داشته باشد، مطالعه می شود.

تابع سوال پاسخ 

تابع سوال پاسخ بر مبنای مدل هایی است که احتمال پاسخ به یک آیتم را به عنوان تابعی از پارامترهای آیتم و زمینه ی فرد برآورد می کند. مدل های سوال پاسخ با توجه به نوع آیتم انواع مختلفی دارد. بر اساس این توابع منحنی سوال پاسخ ترسیم می شود. مدلي كه در ادامه توضيح داده خواهد شد مدل تک بعد لجستیک چهار پارامتری  است که در آن هر آیتم دارای دو طبقه پاسخ  (فعال و نافعال) است. مدل چهار پارامتري بيشترين پارامترهاي موجود در بين مدل هاي مختلف سوال پاسخ را دارا است. در ادامه كار شبيه سازي و انجام آزمايشي پارامتري كردن ژن ها و برآورد پارامترها آنها از طريق مدل سه پارامتري انجام خواهد شد.  

برای روشن شدن موضوع فرض می کنیم K جامعه ی مورد مطالعه داریم که در هر کدام از این جوامع n ژن یکسان مورد تحلیل قرار می گیرند. در هر یک از K جامعه Nk فرد قرار دارد. تابع سوال پاسخ بر اساس مدل چهار پارامتری لوجستیک به صورت زیر است (تاورس و همكاران، 2004):

 

در این مدل 

i= 1,2,….,n ، j= 1,2,….,Nk و k=1,2,….,K

زیتا ϛ نشان دهنده ی پارامترهای آیتم است كه در برگيرنده ي شيب ژن (iα)، پارامتر موقعيت ژن (bi)، پارامتر مينيمم مقدار فعاليت ژن(ci) و پارامتر ماكزيمم مقدار فعاليت ژن (iϒ) است.

Uijk نشان دهنده ی متغییری دو وجهی است که تنها مقادیر یک و صفر را می گیرد. یک به این معنی است که ژن i در فرد j  که متعلق به جامعه یk  است فعال می باشد و مقدار صفر به این معنی است که ژن i در فرد j  که متعلق به جامعه ی k  است نافعال است.

jkƟ نشان دهنده ی زمینه و استعداد  فرد J ام در جامعه ی k ام است.

bi پارامتر موقعیت ژن است که در همان مقیاس زمینه فرد قرار دارد. اين پارامتر سختي فعال شدن ژن را نشان مي دهد.

iα پارامتر شیب یا تمایز ژن i است.

ci ارزش این مقدار بیانگر فعال بودن ژنi  برای کسی است که در زمینه و استعداد بسیار پایینی برای بروز بیماری دارد. به اين پارامتر عرض از مبدا نيز گفته مي شود.

iϒ ارزش این مقدار بیانگر نافعال بودن ژن i برای کسی است که استعداد و زمینه ی بسیار قوی در بروز بیماری دارد. 

D  مقدار مقیاس است که ارزش عددی آن برابر 1.7 می باشد و سبب تبدیل نتایج تابع لجستیک به تابع اجایو نرمال می شود.

N  تعداد افراد حاضر در مطالعه مي باشد.

پارامترها در تابع سوال پاسخ

فرض اساسی تابع سوال پاسخ این است که با افزایش استعداد و زمینه ی فردی امکان بروز و فعالیت یک ژن افزایش پیدا می کند. رابطه ی احتمال فعال (روشن) بودن ژن با توجه به پارامترهای ژن و استعداد افراد در ICC زیر نشان داده شده است. 

 منحنی ویژگی ژن نشان داده شده به شکل S است که مکان یا جایگاه آن و شیب آن توسط پارامترهای ژن مشخص می شود. از آنجا که رابطه ی تکنوا افزایشی از پیش فرض های استفاده از مدل هاي سوال پاسخ است، شیب منحنی ai باید بزرگتر یا مساوی صفر باشد. داشتن شیب مثبت به این معنا است که احتمال فعال (روشن) بودن ژن در افراد با استعداد و زمینه ی بیشتر، بالاتر است. زمانی که مقدار شیب برابر صفر است بر اساس تابع 1: 

 

 

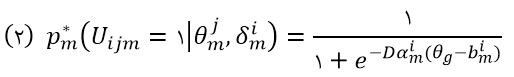
این احتمال برای تمام jkƟ ثابت است یعنی ژن i دخالتی در وقوع بیماری مورد مطالعه ندارد. ممكن است مقدار شيب منفي باشد در اين صورت با افزايش استعداد فرد، احتمال روشن بودن ژن كاهش مي يابد(تاوارس و اندريد ، 2004).

شاید پارامتر bi مهمترین پارامتر در بین چهار پارامتر باشد. هر چه مقدار این پارامتر بزرگتر باشد، احتمال فعال شدن آن توسط یک فرد معين کمتر است. این نتیجه گیری تنها برای شیب های مثبت صادق است. پارامتر Ci و iϒ به ترتیب بیانگر احتمال فعال شدن ژن در فردی با استعداد بسیار پایین و عدم فعال شدن ژن در فردی با استعداد بسیار بالا می باشند(ملينبرگ ، 1994). 

پارامترها در تابع سوال پاسخ
فرض اساسی تابع سوال پاسخ این است که با افزایش استعداد و زمینه ی فردی سطح بيان ژن نيز افزايش پیدا می کند. رابطه ی احتمالي بين سطوح مختلف بيان ژن و ميزان استعداد فرد براي يك ژن كه داراي 5 سطح مختلف بيان است به صورت نمودار زير است.

 

 

 

 

 

 

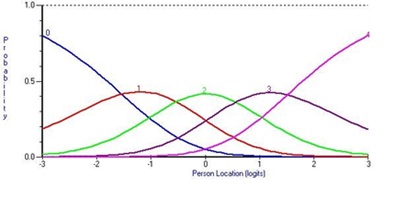
منحنی ویژگی ژن در سطوح مختلف متفاوت است که مکان یا جایگاه آن و شیب آن توسط پارامترهای ژن مشخص می شود. از آنجا که رابطه ی تکنوا افزایشی از پیش فرض های استفاده از مدل هاي سوال پاسخ است،
پارامتر b پارامتري دشواري ژن ناميده مي شود و جايگاه نمودار سطوح بيان را نشان مي دهد. هر چه این پارامتر بزرگتر باشد احتمال فعال شدن آن توسط یک فرد معين کمتر است. در نمودار بالا پارامتر b سطح 5 بيان ژن بيشتر از ساير سطوح است و احتمال پاسخ فرد به اين سطح كمتر از ساير سطوح است. به اين پارامتر جايگاه يا موقعيت گفته مي شود و جايگاه منحني را در نمودار مشخص مي نمايد.
پارامتر α به پارامتر شيب معروف است و بيانگر شيب منحني ها در هر سطح است. همانطور كه در نمودار بالا مشاهده مي شود اين مقدار در سطوح مختلف متفاوت است. براي سطح اول مقدار شيب مثبت و براي سطح آخر مقدار آن مثبت است ولي در سطوح مياني مقدار آن مثبت و منفي است. پارامتر آلفا شكل منحني را مشخص مي كند.
براي درك بهتر نقش پارامترها در تعيين مقادير احتمال در سطوح مختلف فرض مي كنيم دو فرد با استعداد ابتلاء به بيماري 2+ و 2- وجود دارند. بر اساس نمودار فردي كه مقدار استعداد وي برابر 2- است بيشترين احتمال پاسخ وي به يك ژن مشخص سطح اول است و فردي كه مقدار استعداد وي براي 2+ است بيشترين احتمال پاسخ وي به سطح پنجم بيان ژن است. بنابراين هر چه استعداد فرد افزايش يابد احتمال پاسخ وي به سطوح بالاي بيان ژن افزايش مي يابد.

تک بعدی بودن و استقلال موضعی 

یک مفروضه ی مشترک مدل های تک بعد سوال پاسخ آن است که فقط یک استعداد یا زمینه به وسیله ی مجموعه ژن ها اندازه گیری شود. این مفروضه به طور کامل نمی تواند برآورده شود، چرا که همواره عواملی وجود دارند که علاوه بر استعداد مورد نظر بر ژن ها تاثیر می گذارند. آنچه برای برقراری مناسب مفروضه تک بعدی بودن در مجموعه ای از داده های مربوط به ژن ها ضروری است، حضور عامل یا مولفه ای غالب است که عملکرد ژن را برای فرد مشخص می کند. به بيان ديگر تك بعدي بودن به اين معني است که تنها عاملی که باعث می شود Uijk یک یا صفر شود، عامل زمینه ی فردی است.

 وقتی استعداد آزمودنی های مختلف که عملکرد ژن ها را تحت تاثیر قرار می دهند، با یکدیگر برابر باشد، پاسخ آزمودنی ها به هر زوجی از ژن ها به لحاظ آماری ناهمبسته باشد. یعنی بعد از به حساب آوردن زمینه و استعداد افراد هیچ رابطه ای میان پاسخ آزمودنی ها به ژن های مختلف وجود نخواهد داشت. به اين مفروضه استقلال موضوعي گويند. این بدان معنی است که استعدادهای مشخص شده در مدل، تنها عواملی هستند که عملکرد آزمودنی را مشخص می سازد. این مجموعه استعدادهاي کامل فضای مکنون را معرفی می کنند. وقتی مفرضه تک بعدی بودن برقرار است، فضای کامل مکنون تنها عبارت از یک استعداد است.

نامتغير بودن پارامترها

بنا بر نظريه ي سوال پاسخ، پارامترهاي ژن در بين گروههاي مختلف نامتغير است. به بيان ديگر اگر اين پارامترها در گروههاي نمونه مختلف برآورد شود، بايد مقادير يكساني داشته باشند. زيرا بنا بر تعريف، چنانچه قسمتي از خم ويژه ي ژن معلوم باشد مي توان بقيه ي آن را كه مقادير مورد انتظار است را به دست آورد(سالاسانان و بومنسان ،1978). بنابراني پارامترهايي كه براي ژن بدست مي آيد وابسته به گروه نمونه يا آزمودني هايي كه پارامترهاي از طريق آنها برآورد شده است، نمي باشد (بيكر و كيم ، 2004). اين ويژگي يكي از مهمترين مزيت هاي نظريه ي سوال پاسخ محسوب مي شود(لرد ، 1980) و موجب كاربرد پذيري بالاي مدل هاي تحت اين نظريه است. 

نامتغير بودن نه تنها براي پارامترهاي ژن برقرار است بلكه در مورد پارامتر استعداد آزمودني نيز صادق است. با توجه به اين نظريه تفاوت نمي كند استعداد فرد (به عنوان مثال استعداد فرد براي ابتلا به يك بيماري) از طريق كدام مجموعه ژن (مجموعه ژن هاي مرتبط به يك بيماري) اندازه گيري مي شود. مقدار اين استعداد از طريق هر مجموعه اي يكسان است. 

نامعین بودن  مقیاس اندازه گیری

با توجه به این که زمینه ی فردی مقداری بین منفی بینهایت تا مثبت بی نهایت دارد باید مقیاس و واحدی مشخص برای آن در نظر گرفت تا نامعین بودن حذف شود. زمانی که تنها یک جامعه مورد اندازه گیری است مقیاس اندازه گیری با توجه به میانگین و انحراف استاندار صفت در جامعه تعریف مي شود. زمانی که جوامع مختلف مقایسه می شوند یکی از جوامع به عنوان جامعه ی مرکزی و مرجع در نظر گرفته می شود و سایر جوامع با این جامعه مقایسه می شوند. به عنوان مثال جامعه ی افراد سالم می تواند جامعه ی مرجع باشد و سایر جامعه های بیمار با این جامعه مقایسه شوند(فاكس ، 2010). 

برآورد پارامترهاي مدل

 یکی از مهمترین مراحل در نظریه ی سوال پاسخ برآورد پارامترهای ژن هاي مختلف و زمینه ی فردی نمونه ي زيستي است. در مدل هاي سوال پاسخ معمولا پارامترهاي آيتم از طريق روش بيشينه درستنمايي برآورد مي شود. رايج ترين روش هاي مورد استفاده عبارتند از: الف) بيشينه درستنمايي مشترك يا همزمان ب) بيشينه درستنمايي كناري يا حاشيه اي ج) بيشينه درستنمايي شرطي و اگر اطلاعات پيشين وجود داشته باشد مي توان روش هاي بيزي را براي بيشينه درستنمايي همزمان و بيشينه درستنمايي حاشيه اي بدست آورد (رجوع شود به بيكر و كيم، 2004 ) 

در برآورد پارامتر ژن ها ممكن است سه حالت مختلف ممكن است وجود داشته باشد الف) پارامتر ژن ها معلوم باشد و هدف برآورد پارامتر استعداد نمونه زيستي  باشد ب) پارامتر استعداد نمونه زيستي مشخص بوده و هدف برآورد پارامترهاي ژن است و ج) نه پارامتر ژن ها و نه پارامتر استعداد مشخص است. در بيشتر مواقع پارامتر ژن ها و افراد هر دو نامشخص اند و لازم است اين پارامترها به طور همزمان برآورد شوند. 

مطالعه ي شبيه سازي شده 

در اين بخش متدولوژي مطالعه ي زمينه و استعداد فرد و پارامتري كردن  ژن ها از طريق داده هاي شبيه سازي شده نشان داده مي شود. اين مطالعه به ما كمك مي كند تا بتوانيم روند استفاده از نظريه سوال پاسخ در مطالعات زيست شناسي ملكولي و ژنتيك نشان دهيم. به منظور انجام مطالعه ي شبيه سازي از مدل سه پارامتري سوال پاسخ استفاده مي شود. مدل هاي ديگر سوال پاسخ مانند مدل پاسخ مدرج  به دليل انطباقي كه با سطوح بيان ژن دارند، مي توانند موضوع مطالعات بعدي باشند. علاوه بر اين در صورت دسترسي به داده هاي واقعي مي توان مطالعه را با داده هاي واقعي انجام داد. استفاده از ساير مدل هاي سوال پاسخ مخصوصا مدل هاي چند بعدي سوال پاسخ  نيز مي تواند در مطالعات بعدي مورد نظر پژوهشگران باشد. 

فرض مي كنيم كليه ي اطلاعات موجود، آگاهي از وضعيت خاموش يا روشن (صفر و يك) بودن 10 ژن مختلف در 5000 نفر است كه استعداد و زمينه آنها در روشن و يا خاموش كردن ژن ها متفاوت است. وضعيت خاموشي يا روشني ژن به سطح استعداد افراد وابسته است و يك رابطه ي تكنوا  بين آنها وجود دارد. براي دستيابي به اين داده ها مي توان از نرم افزار  wingen (هان ، 2007)  استفاده كرد. اين نرم افزار بر اساس ويژگي هاي گروه نمونه و پارامترهاي ژن، داده هاي خام  را توليد مي كند. توزيع استعداد گروه نمونه در فعال كردن ژن و پارامترهاي مربوط به ژن ها در جدول 1 نشان داده شده است. داده هاي نهايي مبتني بر اين ويژگي ها با 2000 تكرار بدست آمده اند. همانطور كه ذكر شد، مدل در نظر گرفته شده براي انجام آزمايشي در اين مطالعه بر مبناي داده هاي شبيه سازي شده، مدل سه پارامتري است. مقدار پارامتر عرض از مبدا براي تمام ژن ها 0.1 در نظر گرفته شده است.

جدول 1: آماره هاي توصيفي مربوط به توزيع استعداد گروه نمونه و پارامتر ژن ها

 گروه نمونه پارامتر دشواري پارامتر شيب

تعداد50001010

نوع توزيع نرمالنرمالنرمال

ميانگين 001

انحراف استاندارد110.2

بر اساس جدول بالا نرم افزار داده هاي تصادفي مبتني بر توزيع مشخص شده توليد مي كند.  ارزش نهايي پارامترهاي بدست آمده از طريق نرم افزار براي 10 ژن در جدول زير نشان داده شده است.

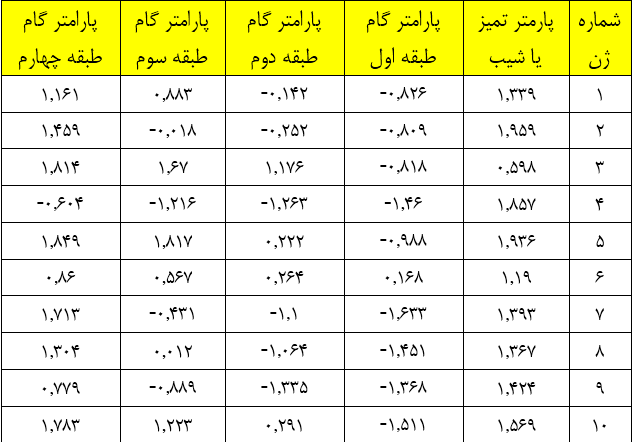
نرم افزار بعد از 2000 تكرار ، داده هاي خام مربوط به 5000 مورد نمونه كه در واقع الگوي پاسخ آنها به 10 ژن مختلف است را ارائه مي دهد. در موقعيت هاي واقعي تنها اطلاعات موجود الگوي پاسخ  افراد به ژن هاي مختلف است. بنابراين فرض مي شود براي برآورد پارامتر سوالات و يا سطح استعداد و زمينه ي موارد زيستي، داده ها از موقعيت هاي واقعي بدست آمده اند. 

الگوي پاسخ به عنوان ورودي به نرم افزار هاي سوال پاسخ (در اينجا نرم افزار بايلوگ ام جي ) وارد مي شوند تا پارامتر ژن ها و استعداد افراد برآورد شوند. خروجي نهايي مربوط به پارامتر سوالات از نرم افزار بايلوگ در جدول 2  نشان داده شده است. 

جدول 2: ارزش برآورد شده پارامتر ژن ها

 

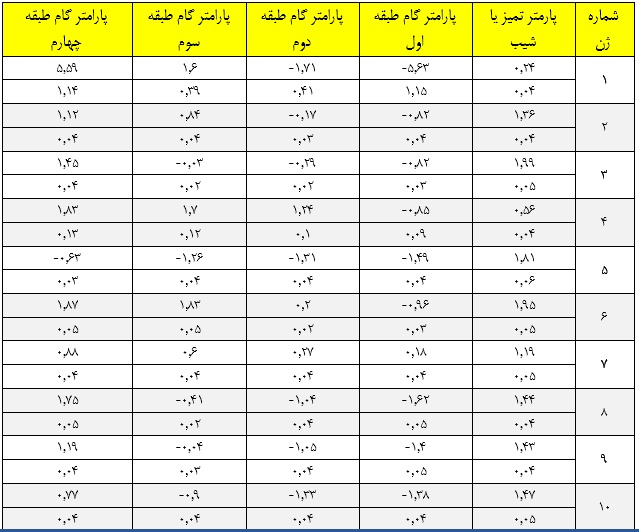
علاوه بر اين خروجي منحني هاي ويژگي ژن  مي تواند در مطالعات ژنتيك مورد استفاده قرار بگيرد. ماتريس نمودار ويژگي 10 ژن مورد نظر در شكل زير نشان داده شده اند. 

نمودار 1: نمودار ويژگي ژن ها

 

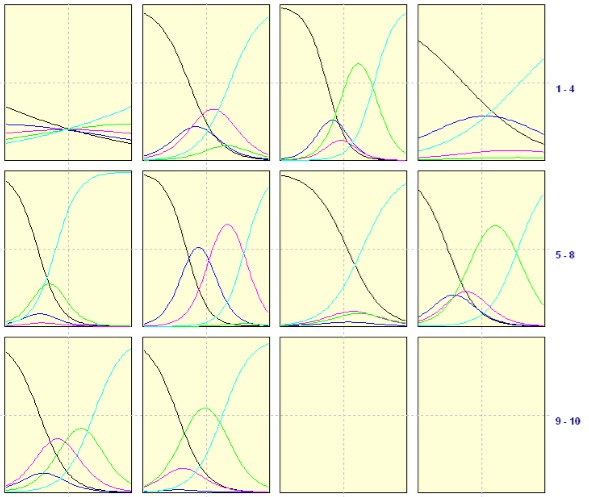
محور x در اين نمودارها استعداد يا زمنيه ي فرد يا نمونه ي زيستي است و محور y احتمال فعال شدن يك ژن مشخص مي باشد. همانطور كه مشاهده مي شود تمام نمودارها تكنوا افزار بوده و با افزايش استعداد فردي احتمال فعال كردن ژن نيز افزايش مي يابد. 

بر اساس اين روش استعداد 5000 هزار نفر در فعال سازي ژن هاي مورد مطالعه بدست آمده اند. به دليل حجم بالاي نتايج از ذكر آنها در اينجا خودداري مي شود. در صورتي كه نياز باشد مطالعه روي فرد خاصي صورت پذيرد مي توان به استعداد يا زمنيه ي فردي وي پي برد.

نتيجه گيري

در اينجا روش جديدي به منظور دست يابي به ويژگي ژن ها مبتني بر سه پارامتر مختلف و برآورد استعداد افراد در فعال سازي ژن ها معرفي شد. فعال سازي مي تواند به ژن هايي مربوط شود كه موجب يك بيماري خاص، و يا عامل يك بروز يك صفت ويژه مي شود. علاوه بر اين روش پيشنهادي مي تواند در مدرج سازي ژن هاي مختلف استفاده شود و به اين ترتيب بانك ژن  بر اساس پارامترهاي مطرح شده تشكيل شود. تشكيل بانك ژن مي تواند در پژوهش هاي مربوط به حوزه هاي مختلف علوم پزشكي استفاده شود.  

از طريق داده هاي شبيه سازي شده مراحل پارامتري كردن ژن ها توضيح داده شد. مدل مورد استفاده در اين مطالعه مدل سه پارامتري سوال پاسخ است كه مي توان در مطالعات بعدي از مدل هاي ديگر مانند مدل پاسخ مدرج و يا مدل چند بعدي سوال پاسخ استفاده نمود. از آنجا سطح بيان ژن را مي توان حداقل به صورت ترتيبي مشخص كرد و طبقات ترتيبي براي آن تعريف نمود، بنابراين استفاده از مدل هاي چند ارزشي سوال پاسخ مي تواند به اطلاعات بيشتري از ژن ها منجر شود. 

منابع

Borsboom, D. (2005). Measuring the mind: Conceptual issues in contemporary psychometrics.Cambridge: Cambridge University Press.

Borsboom,D.(2008). Latent variable theory. Measurement, 6,25-53.

Hambleton, R. K., & Swaminathan, H. (1985). Item Response Theory: Principles and applications.Boston:Kluwer-Nijhoff.

Tavares, H. R., Anderade, D.,F., & Braganca Pereira, C. A.(2004). Detection of determinant genes and diagnostic via Item Response Theory. Genetics and molecular biology, 27,679-685.

Mellenbergh,G.J.(1994).Generalized Linear Item Response Theory. Psychological Bulletin, 115, 300–307.

Sanathanan,L., and Blumenthal, N. (1978) The logistic model and estimation of latent structure. Journal of the American Statistical Association 73:794-798.

Baker, Frank B.; Kim, Seock-Ho (2004). Item Response Theory: Parameter Estimation Techniques (2nd ed.). Marcel Dekker. ISBN 978-0-8247-5825-7.

Lord FM (1980) Applications of Item Response Theory to Practical Testing Problems. Lawrence Erlbaum Associates, Inc., Hillsdale.

Fox, Jean-Paul (2010). Bayesian Item Response Modeling: Theory and Applications. Springer. ISBN 978-1-4419-0741-7.

Han, K. T. (2007).  WinGen2: Windows software that generates IRT parameters and item responses [computer program]. Amherst, MA: University of Massachusetts, Center for Educational Assessment. Retrieved May 13, 2007, from http://www.umass.edu/remp/software/wingen/

Tavares, HR. & Andrade DF (2004) Item response theory for longitudinal data: Item and population ability parameters estimation.