تحلیل و مدلبندی شبکه های مغزی در حوزه ی علوم اعصاب و رفتار
در سال های اخیر مطالعه ی شبکه ها به صورت گسترده ای در حوزه های مختلف علمی مانند حوزه ی علوم اجتماعی، اقتصاد، سیستم های زیستی، علوم اعصاب، علوم شناختی و رفتاری گسترش یافته است. اصلی ترین دلیل رشد رویکردهای شبکه ای ارتباطات بین سیستم های مختلف و ظهور و گسترش سیستم های پویا است که از طریق مجموعه ای از تکنیک های آماری و ریاضیاتی که خاستگاه آنها نظریه ی گراف است، قابل تببین و توصیف و تحلیل است. کاربردهای نظریه گراف حوزه ی وسیعی را در بر می گیرد. از این نظریه در برنامه ریزی شهری، کنترل ترافیک، همه گیر شناسی، برنامه ریزی مالی، موتورهای جستجوی اینترنت، تحلیل سیستم های زیستی پیچیده محیطی و مولوکولی و روانسنجی استفاده می شود. فعالیت های زیادی روی معماری شبکه، پویایی و همچنین رشد فرآیندهای آن انجام شده است. در حالی که بیشتر نظریه ی گراف کلاسیک به تحلیل گراف های تصادفی می پردازند، علم مدرن شبکه، روی سیستم های جهان واقعی متمرکز است و نشان داده است که شبکه های واقعی در اکثر موارد، تصادفی نیستند. این شبکه ها سازمان هایی با فرآیندهای بنیادی زیر بنایی اند که ضامن بقا، رشد و ساختار آنها می باشند.
درک و فهم سازمان شبکه ای به پیچیدگی مغز، در اولین گام مستلزم فهم عملکرد آن به عنوان یک سیستم یکپارچه است. نتایج تلاش های نقشه بندی مغز و تکنیک های رکورد آن در کنار فعالیت های علمی که به صورت اختصاصی به ارتباطات مغزی می پردازند، مجموعه داده هایی از ارتباطات وسیع مغز گردآوردی کرده است. این داده های نشان می دهند که برای تحلیل، نیازمند تحلیل های کمی و ابزارهای مدلبندی جدید به منظور آشکارسازی ویژگی های سازمان شبکه مغز می باشند.
با وجود این که روش های گوناگون و متعددی برای مشاهده ی آناتومی و فیزیولوژی مغز وجود دارد، جای تعجب نیست که ابزارهای متعددی نیز به منظور تعریف ارتباطات مغزی و رکورد آنها وجود داشته باشد. به طور کلی سه نوع ارتباط مغزی موجود است: ارتباطات ساختاری، ارتباطات عملکردی و شیوه هایی که ارتباط و تعامل این دو نوع را به یکدیگر مربوط می سازند. ارتباطات ساختاری به مجموعه ای از ارتباطات فیزیکی بین مولفه های عصبی مانند ارتباطات سیناپسی یا مسیرهای متوالی فیبری اشاره دارد. ارتباطات عملکردی الگوهای تعاملی پویایی هستند که معمولا از طریق داده های سری زمانی عصبی (مانند همبستگی های متقاطع، اطلاعات تعاملی یا همگنی درونی) بدست می آیند. شیوه های موثر رابط و تسهیل کننده ی رابطه ی ساختار و عملکرد مغز، شبکه ای از تاثیر و تاثرات علی بین مولفه های عصبی را شامل می شود و اغلب بر اساس سرنخ هایی که از سری های زمانی یا بر اساس مداخلات آزمایشی بدست می آیند، کشف و مطالعه می شوند.
در حالی که ارتباطات ساختاری (حداقل در مقیاس زمانی ثانیه تا دقیقه) تا حدی ثابت باقی می مانند، ارتباطات عملکردی و شیوه های موثر، می توانند در کسر بسیار کوچکی از ثانیه هم به صورت خودکار و هم زمانی که فعالیت عصبی برانگیخته می شود، تغییر کنند و ساخت جدیدی پیدا کنند.
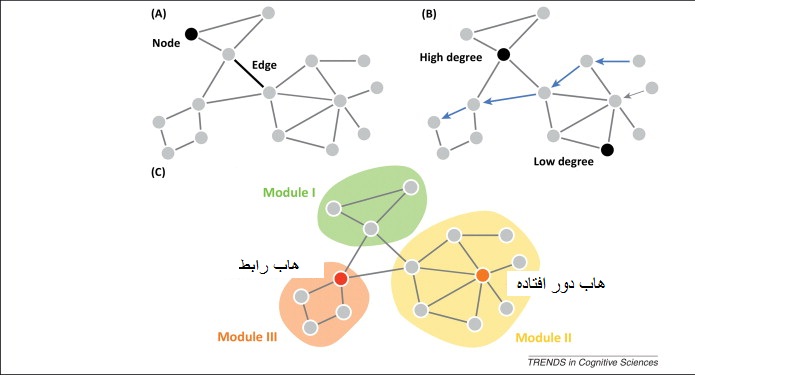
وجه مشترک تمام ارتباطات مغزی این است که می توان آنها را از طریق شبکه یا گراف نشان داد و تحلیل نمود. گراف ها زبان ریاضی سیستم هایی هستند که مولفه های آن ارتباطات درونی دارند و با گره ها و یال ها در نظریه گراف قابل مقایسه اند. گره ها ماهیت های عملکردی بنیادین سیستم می باشند و در مغز گره ها می تواند نرون ها به تنهایی، جامعه ی نورونی یا نواحی مغزی باشند. یال ها ارتباطات و اتصالات بین گره ها هستند. در شبکه مغز این ارتباطات می تواند سیناپس ها یا مسیرهای متوالی فیبری و یا روابط علی یا آماری باشند که شباهت، مجاورت یا ارتباط عملکردی را توضیح می دهند. مجموعه ی کامل گره ها و یال ها را می توان از طریق ماتریس ارتباطات که به ماتریس مجاورت مشهور است، نشان داد. این ماتریس نشان می دهد که کدام زوج از گره ها مجاور یکدیگرند.
مفهوم بنیادین دیگر مربوط به نظریه گراف در شبکه مغزی، مسیر عصبی است: منظور از مسیر، یال های متوالی است که به صورت غیر مستقیم یک گره را به گره دیگر مرتبط می سازند. طول کوتاهترین مسیر بین دو گره به عنوان فاصله بین آن دو گره در نظر گرفته می شود و به عنوان حداقل تعداد یالی تعریف می شود که یک گره را به گرهی دیگر وصل می کند. توجه کنید که در گراف ها، فاصله به عنوان فاصله توپولوژیکی بین دو گره تعریف می شود نه به عنوان فاصله در فضای متریک.
شبکه مغزی وابسته به روش رکورد آن یا بر اساس سیستم آزمایشی بکار گرفته شده در مطالعه تجربی، می تواند به روش های مختلفی استخراج شود. اولین گام تعریف گره ها و یال های شبکه است. این گام نه تنها اولین گام بلکه مهمترین گام نیز به شمار می رود. تحلیل آماری شبکه مغزی مبتنی بر تعریفی است که بر اساس آن سیستم زیستی به گره و یال تقسیم بندی می شود. در سیستم های بزرگ مقیاسی مانند مغز، تعریف گره در برگیرنده تقسیم بندی مغز به نواحی یکپارچه بر اساس داده های تصویری و هیستولوژیک است. روش های بخش بندی مستخرج از داده نیازمند حوزه ی فعالی از پژوهش است و در حال حاضر با چالش های جدی روبرو است. روش های خوشه بندی منجر به پردازش های با اعتبار بالا در شبکه مغزی شده است. در این روش ها شباهت بین نیمرخ ارتباطات ساختاری یا عملکردی به منظور استخراج محدوده های بین نواحی مختلف مغز، بدست می آید.
گام های نظری تحلیل گراف به صورت زیر است:
الف) تعریف گره های شبکه ب) برآورد اندازه ای مناسب از ارتباط ج) ساخت ماتریس ارتباطات و د) تحلیل نظری گراف مربوط به شبکه ی استخراج شده.
بعد از تعریف گره ها، تعریف یال های معمولا در برگیرنده ی برآوردهای ارتباطات جفتی بین گره ها است. شبکه های ساختاری بر مبنای مسیرها و تراکت های فیبری اندازه گرفته شده، ساخته می شوند. در حالی که یال های موثر و عملکردی اغلب بر مبنای ارتباطات آماری برآمده از داده های سری زمانی تعریف می شوند. اندازه های ارزشمندی برای نشان دادن جفت های عملکردی وجود دارد. در حالی که بیشتر مطالعات به منظور تعریف ارتباطات عملکردی از اندازه های ساده ای مانند همبستگی استفاده می کنند، استراتژی های پیچیده تری مانند همبستگی های تفکیکی و نیمه تفکیکی یا ارتباطات جهتدار (علی) و تعاملی را نیز می توان به کار گرفت.
زمانی که یک شبکه مغزی شکل می گیرد، می تواند از طریق ابزارهای کمی برآمده از نظریه ی گراف تحلیل شوند. بسیاری از این روش ها و ابزارها در اختیارند که می توانند در حوزه ی علوم اعصاب و رفتار به کار گرفته شوند. قبل از این که رویکردهای نظری گراف به گستردگی استفاده شود، مفاهیم روش شناسی مهمی نیازمند بررسی است.
اگر بخواهیم اندازه های بدست آمده از نظریه گراف را در مورد شبکه ی مغزی دسته بندی کنیم، سه طبقه مختلف از اندازه های گراف وجود دارد که جنبه های مختلفی از سازمان شبکه ای مغز را متمایز می سازند:
الف) وجود ارتباطات و ماژول های اختصاصی شده (جداسازی عملکردی).
ب) الگوی تعاملات کلی بین ارتباطات (یکپارچه سازی عملکردی)
ج) اثر عملکردی عناصر شبکه های فردی (اثرات عملکردی).
جداسازی عملکردی: خوشه بندی و ماژول بندی
یکی از موارد مهم در پردازش ویژگی های گرهها و توزیع عملکردی آنها تعاملاتی است که با همسایگان نزدیکشان دارند. در واقع مجموعه ای از گره ها وجود دارند که به صورت مستقیم با هم در ارتباطند. مطالعات بسیار زیادی که در زمینه ی شبکه های مغزی انجام شده است؛ نشان می دهد که نواحی عصبی وجود دارند که در آن نواحی خوشه ها و ارتباطات متقابل و زیادی وجود دارد، که به آن همسایگان می گویند.
ضریب خوشه بندی یکی از اندازه های ابتدایی برای مشخص کردن درجات گره ها در ارتباطات منطقه ای می باشد. خوشه بندی یک گره زمانی بالا است که همسایگان هر گره همسایه ی یکدیگر باشند. به طور میانگین در تمام شبکه ضریب خوشه بندی نشان دهنده ی درجه ای از شبکه است که ارتباطات محلی بین گره های مختلف آن را نشان می دهد. از آنجا که خوشه بندی خیلی به اندازه و چگالی هر یک از شبکه ها وابسته است، لازم است از علم آمار به منظور تولید شبکه های تصادفی به منظور مقایسه ی معناداری شکل گیری خوشه ها استفاده شود.
در بسیاری از موارد خوشه بندی بالا نشان دهنده ی ارتباطات چندگانه و بخش بخش گره های مختلف است. این ارتباطات و ماژول ها را می توان از طریق الگوریتم هایی که به دنبال بخش بندی کردن شماها هستند، پیدا کرد. این شماها به صورت بهینه شبکه را به زیر شبکه هایی تقسیم می کند و اندازه هایی از بخش بندی یا ماژولبندی ارائه می دهند. یکی از شاخص ها چگالی نسبی درون ماژول نسبت به چگالی ارتباطات بین ماژول های مختلف است. مطالعات زیادی از شبکه های ساختاری و عملکردی مغز انجام شده است که به شناسایی ماژول های مختلف و مشخص کردن حدود و جایگاه انها می پردازد که به شبکه های شناختی یا زیر بخش های عملکردی مغز انسان مشهورند. از طریق گسترش روش های تحلیلی که به منظور بخش بندی استفاده می شوند، پژوهشگران به این نتیجه رسیده اند که بخش ها و ماژول های شبکه های مغزی ساختار سلسله مراتبی دارند. این ویژگی معماری مغز، ترسیم نقشه ی بخش های مختلف مغز را به لحاظ اقتصادی و فیزیکی ارتقا می دهد و تاثیر مهم و معناداری روی پویایی مغز می گذارد.
یکپارچه سازی عملکردی: شاخص های طول مسیر و کارایی
در حالی که بخش بندی و ماژول بندی اطلاعات مهمی را در باره ی ساختار ارتباطی محلی یا منطقه ای مغز ارائه می کند، اندازه های مکملی وجود دارند که گنجایش شبکه در زمینه ی دربرگیرندگی تعاملات کلی تر و گسترده تر از تعاملات منطقه ای و همچنین یکپارچگی فعالیت پویای مغز را نشان می دهند. بعضی از این انداز ها مبتنی بر مسیر می باشند. مخصوصا طول کوتاهترین مسیر که دو گره مختلف را به هم وصل می کند. به طور کلی مسیرهای کوتاهتر به نظر می رسد؛ به صورت کاراتری اطلاعات را انتقال می دهند. بنابراین میانگین طول مسیر برای شبکه می تواند یک شاخص از گنجایش شبکه در تعامل اطلاعات کلی، محسوب شود. یکی دیگر از اندازه های مربوط به این موضوع (که در واقع عکس طول مسیر متوسط است اما کمتر از وجود گره های منفک و جدا شده آسیب می بیند) کارایی کلی است. همانند خوشه بندی، طول مسیر نیز باید از طریق یک آزمون آماری بررسی شود، تا از این طریق به مقادیری معنادار برای حجم و چگالی شبکه دست یافت.
به دلیل اهمیت جریان اطلاعات و ارتباطات در شبکه های مقیاس بزرگ مانند شکبه های مغزی، اندازه ها مربوط به یکپارچه سازی عملکردی، مشخصات زیستی عصبی نسبتا مشخص و روشنی دارند. در یک شبکه با کارایی بالا، مسیرهای ارتباطی کوتاه می توانند بین جفت گره های مختلف مشخص می شوند. با وجود این که خوشه بندی و طول مسیر جنبه های مکملی از شبکه عملکردی سازمان مغز محسوب می شوند، اغلب از طریق اتصال و ارتباط معنی پیدا می کنند. اگر چه این اندازه ها می تواند به منظور سنجش درجه ای از تعادل شبکه بین ارتباطات موجود محلی و ارتباطات بخش بندی شده در کل محسوب شود، می تواند به منظور سنجش یکپارچگی سیستم نیز به حساب آید.
اثرات عملکردی: مرکزیت و هاب ها
شبکه های جهان واقعی در بسیاری از موارد تصادفی نیست و اختلاف معناداری با ساخت های تصادفی دارد. علاوه بر این در بین گره های این شبکه ها روابط معناداری وجود دارد. عناصر شبکه را می توان از طریق مشارکت آنها در شبکه به طبقات مختلفی طبقه بندی کرد. به عنوان مثال بر اساس شیوه ی ارتباطی که با سایر اجزای سیستم دارند، طبقه بندی نمود. یکی از تمایزات مهمی که می تواند بر اساس اثر آنها ساخته شود اثر بالقوه ای است که آنها بر کلیت سیستم می گذارند و گنجایش آنها به منظور انتقال یا پردازش اطلاعات. گره هایی که اثرات بالا دارند اغلب به عنوان هاب شناخته می شوند. شناسایی هاب های شبکه های مغزی برای نقشه بندی نواحی مختلف مغز که بیشترین تعامالات عملکردی را دارند و به یکپارچگی سیستم کمک می کنند، ضرورت دارد. هاب ها می توانند بر اساس تعداد تعاملاتی که در مسیرهای کوتاه شبکه دارند، نیز شناسایی شوند. اندازه ای که از این تعریف بدست می آید به عنوان مرکزیت بینابینی شناخته می شود که برای شبکه های ساختاری اهمیت دارد و همچنین می تواند برای یال ها به خوبی استفاده شود.
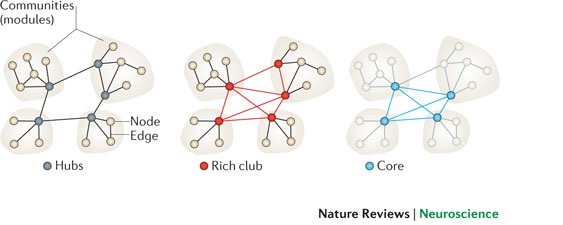
زمانی که یک بخش بندی ماژولی شناخته می شود تنوع ارتباطات گره ها با توجه به ماژولهای اختصاصی می تواند در قالب ضریب اشتراک سنجش شود. یکی از چیزهای مورد توجه این است که گره هایی که ارتباطات بالا دارند، ضریب اشتراک پذیری بیشتری نیز دارند. به این گره ها هاب های ارتباط دهنده گفته می شود. ارتباط بین ماژول های مختلف از طریق این هاب ها انجام می شود. از طرف دیگر گره های با درجه بالا وجود دارند که ارتباطات ماژولی آنها پایین است و بنابراین شاخص اشتراک پذیری آنها کم است. و به همین دلیل به آنها هاب های دور افتاده یا منزوی گفته می شوند چون بیشترین ارتباط آنها، بین خود ماژول شان می باشند.
هاب ها در شبکه ی مغزی خیلی اهمیت دارند. درجهی مرکزیت بالا و ارتباط دهندگی آنها و همچنین اشتراک بالای انها در ارتباطات ساختاری نشان می دهد که آنها نقش بسیار حیاتی در جریان یکپارچه سازی فرآیند ها و جریان اطلاعات دارند. پژوهش ها نشان می دهد که ارتباطات بالایی بین هاب های ذهن انسان، با نواحی درد که نرخ متابولیسم در آن بالا است وجود دارد. این موضوع در مورد بیمارانی که مشکلات عصبی دارند، نیز صادق است. این نتایج می تواند به ایجاد این فرض بیانجامد که توپولوژی مغز با ساختار آن در ارتباط است. علاوه بر این سنجش مرکزیت می تواند به منظور پیش بینی نواقص ساختاری که بر اساس حذف گره یا یال در مغز بوجود می آیند، استفاده شود. در یک بافت زیست عصبی، فقدان گره های مرکزی یا یال ها به ترما یا بیماری منجر خواهد شد.
کاربردهای بیشتری برای نظریه گراف متصور است. روش های گراف وکاربرد آنها در شبکه های با مقیاس بزرگ منجر به ظهر بینش معناداری در عملکرد و سازمان مغز انسان شده است این کاربرد ها گسترده زیادی از شبکه های اناتومی مغز تا ارتباطات عملکردی در نواحی مختلف مغزی را در بر می گیرد. علاوه بر این ارتباطات عملکردی در زمانی که از طریق تکالیف ارائه شده، بر انگیخته می شوند، در بررسیر تفاوت های فردی و جامعه ی بالینی بسیار کاربردی خواهد بود. روش های عینی برای مقایسه شبکه ی مغزی افراد مختلف یا بین جامعه های مختلف، امکان مطالعات طولی مغز و رشد بیماری های مغزی مختلف را فراهم می آورد. رویکردهای شبکه ای جنبه های مختلفی از شبکه های مغزی را روشن کرده اند. به عنوان مثال این مطالعات تغییرپذیری معناداری را در ارتباطات ساختاری و عملکردی مغز نشان می دهند. بررسی تغیرپذیری ارتباطات بین شبکه های مختلف مغزی یکی از حوزه های مهم برای پژوهش های آینده در حوزه ی شناختی و رفتاری است.
 به نام یزدان پاک
به نام یزدان پاک